Component 1: Binomial-Poisson Mixture

The first component of this model is a binomial-Poisson mixture:

\[n_{t,j,s} \sim binomial(N_{t,j,s}, p_{t,j,s})\] \[N_{t,j,s} \sim Poisson(\lambda_{t,j,s})\] \(n_{t,j,s}\) is the recorded number of groups (for non-solitary species; more on this later) or counts (solitary species) during replicate \(t\) of transect \(j\) for species \(s\). This is data! \(N_{t,j,s}\) is the latent number of groups (non-solitary) or abundance (solitary), \(p_{t,j,s}\) is detection probability, and \(\lambda_{t,j,s}\) is the expected number of groups (non-solitary) or abundance (solitary).

Here is the code:

n[t,j,s] ~ dbin(N[t,j,s], pcap[t,j,s])
N[t,j,s] ~ dpois(lambda[t,j,s])

The binomial part of this mixture is to link what we see/observe in the field to the actual biological process by accounting for imperfect detection. The second part of the mixture is accounting for stochasticity in latent abundance (or number of groups) by describing it as a random Poisson variable.

Component 2: Imperfect Detection & Distance Sampling

This first component is similar to an N-mixture model, but instead of detection probability being estimated from repeated surveys, it is estimated by a detection function using recorded distances. A variety of detection functions exist (Buckland et al. 1993), but they all have one trait in common, which is that detection probability descreases as a function of distance from the transect.

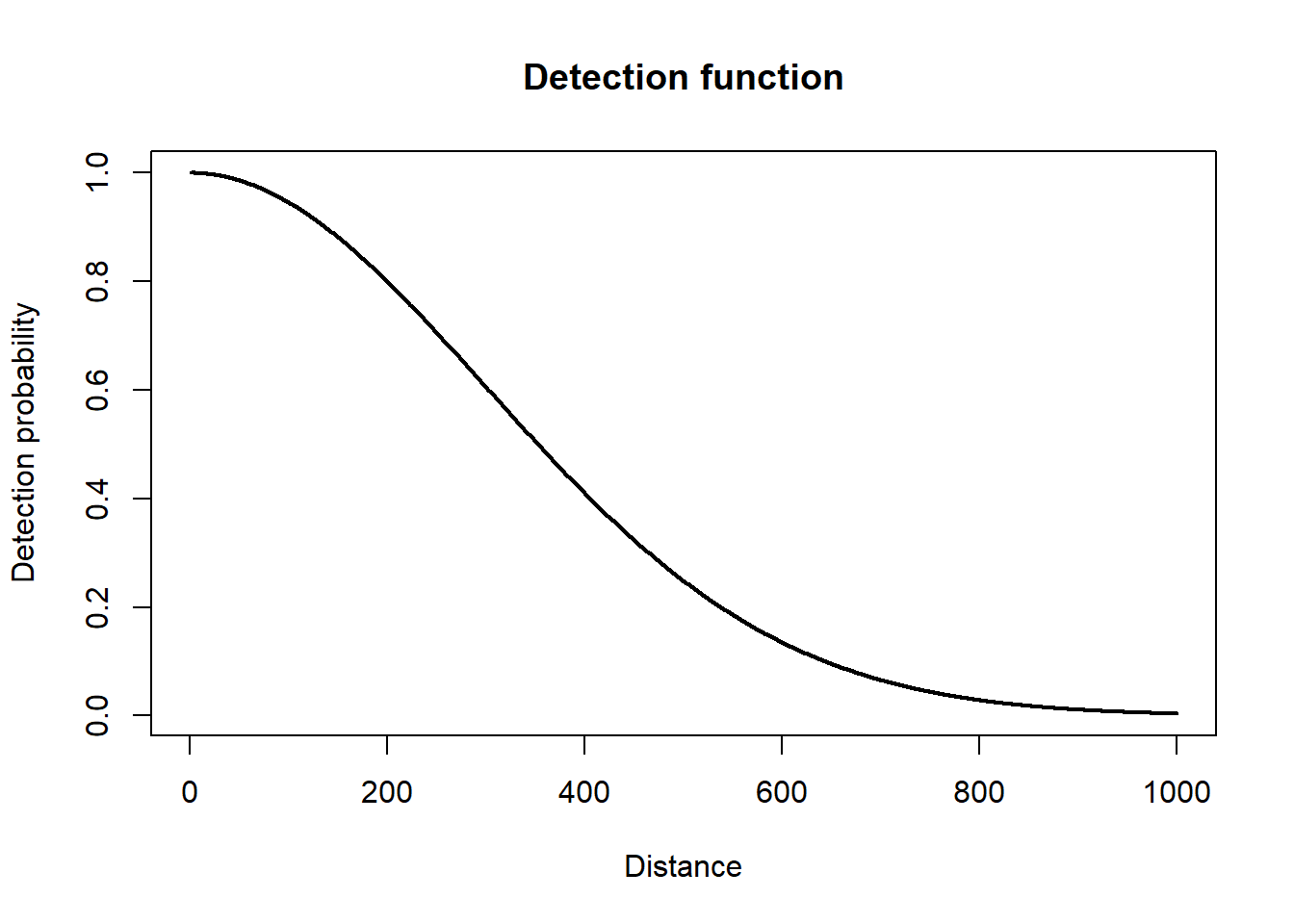
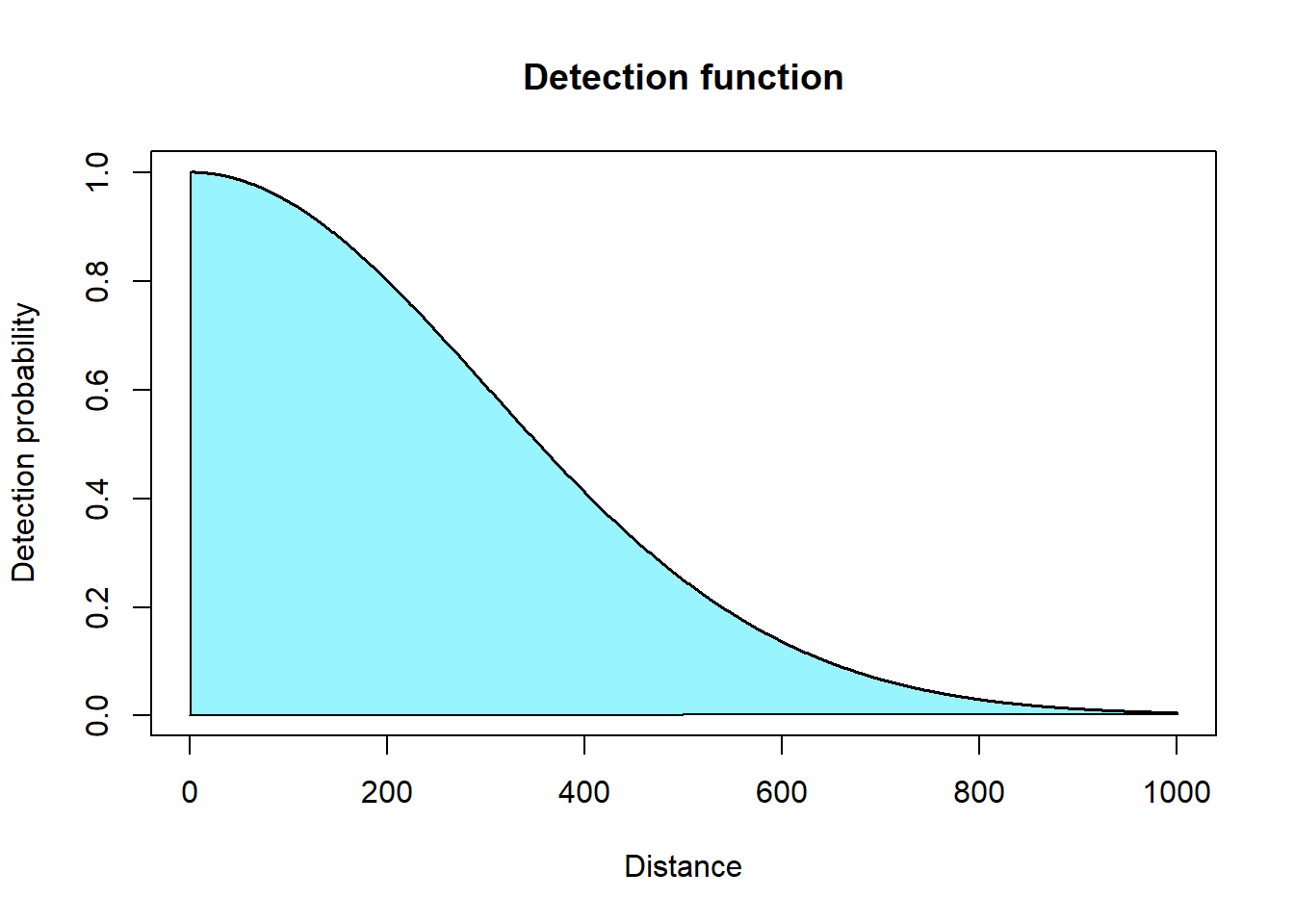
To calculate detection probability you integrate the detection function to find the area under the curve.

However, we find it more convenient to approximate this integral using distance bins (i.e., multiple rectangles).

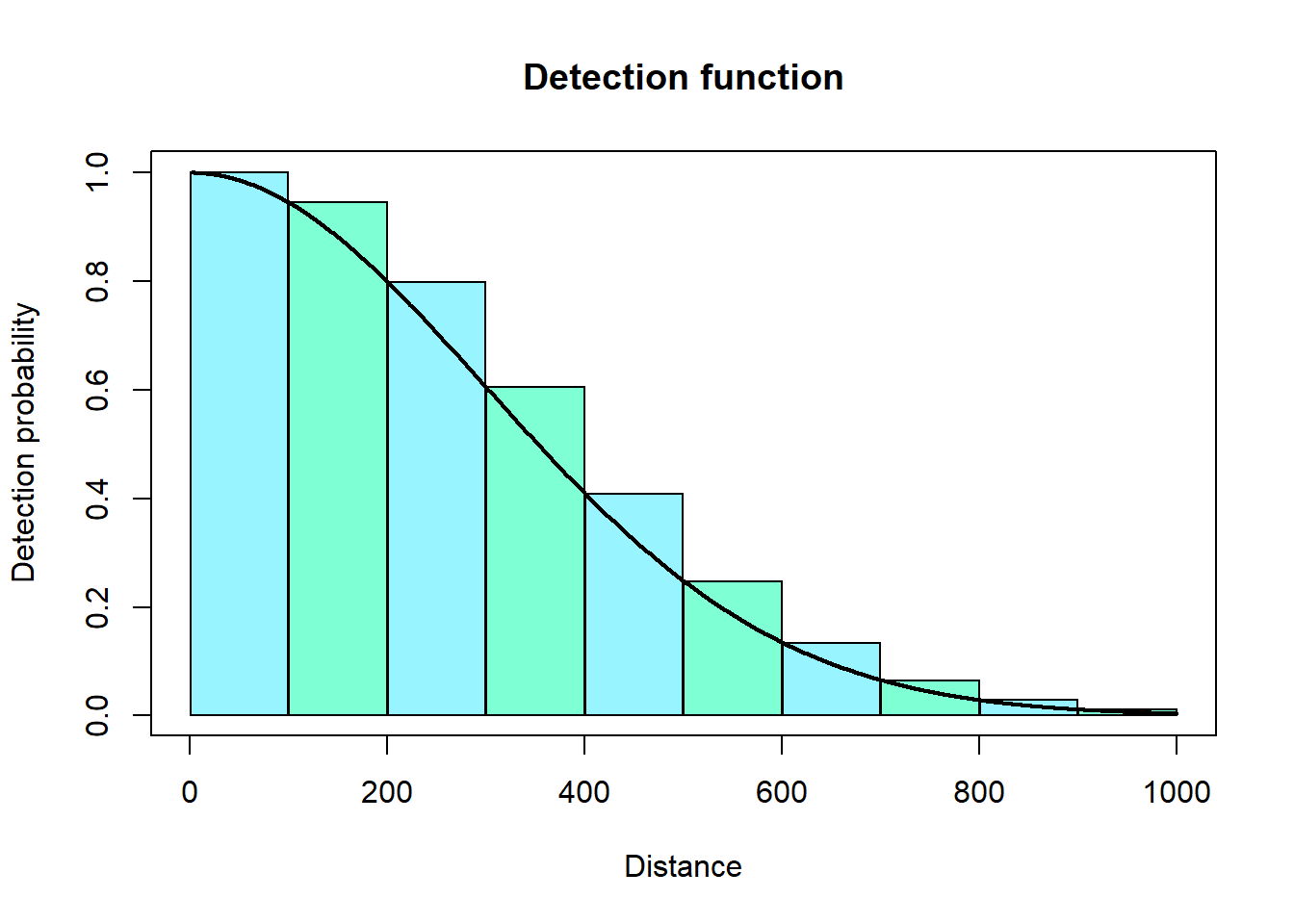
We can then sum up the areas of these rectangles to approximate the area under the curve. The code for this looks like:

g[k,t,j,s] <- exp(-mdpt[k]*mdpt[k]/(2*sigma[j,s]*sigma[j,s]))
pi[k,t,j,s] <- v/B
f[k,t,j,s] <- g[k,t,j,s] * pi[k,t,j,s]

Here g is the height of each rectangle k (t = rep, j = site, s = species) and pi is the width of each rectangle. mdpt[k] is the distance at the midpoint of each class, which is data. sigma is the scale parameter of the half-normal distribution, which we are trying to estimate. v is the length of each distance class (the same for each of the distance classes in our case). B is the transect half-width. We can then sum f up as follows:

pcap[t,j,s] <- sum(f[1:nD,t,j,s])

We now need to link these rectangles to our model to be able to estimate them. We do that by splitting our observations, \(n_{t,j,s}\), into each distance class \(k\) giving us \(y_{k,t,j,s}\). The vector of observation across distance classes, \(\mathbf{y_{t,j,s}}\), is the realization of a multinomial distribution: \[\mathbf{y_{t,j,s}} \sim multinomial(n_{t,j,s}, \mathbf{\pi^c_{t,j,s}})\] \(\mathbf{\pi^c_{t,j,s}}\) is the vector of detection probabilities at each distance class (not the same pi as above in the code). The key here is that \(\mathbf{y_{t,j,s}}\) and \(n_{t,j,s}\) are data, so we can easily estimate \(\mathbf{\pi^c_{t,j,s}})\).

We use the categorical distribution within JAGS instead of the multinomial as it is more flexible (See Kéry & Royle 2016, pg. 453). The code for this looks like:

dclass[i] ~ dcat(fc[1:nD, rep[i], site[i], spec[i]])

This links the distance for each observation to the conditional detection probability, fc. fc is the area of the rectanlge divided by the total area under the curve:

fc[k,t,j,s] <- f[k,t,j,s]/pcap[t,j,s]

Component 3: Group Size

The next component of our model is for group sizes. Often we see individuals of a certain species within a group. These observations violate the assumption of independence. Thus we aggregate these observations by referring them as a group with a group size greater than 1. We can then model the group sizes separately to estimate an average group size and mulitply it by the number of groups to derive abundance. The code for group sizes is:

gs[i] ~ dpois(gs.lambda[s.rep[i], s.site[i], s.spec[i]]) T(1,)

gs[i] is the observed group size for a specific observation. We then connect this to the replicate, site, and species. gs.lambda is the average group size for a specific replicate, site, and species.

Component 4: Linear Predictors

We now have the basic distance sampling structure and can move on to estimating variation in expected abundance (or number of groups). We use the log-link function and a linear predictor made up of covariates explaining variation in abundance.

lambda[t,j,s] <- exp(alpha0[s] + ...)

We can also model variation in group size:

gs.lambda[t,j,s] <- exp(beta0[s] + ...)

Or detection probability:

sigma[j,s] <- exp(gamma0[s] + ...)

Component 5: Community Hyper-distributions

To make this a multispecies model, we link parameters within each of the linear predictors above using a random effect by species. We allow for each parameter to have a common or community hyper-distribution with corresponding hyper-parameters (e.g., \(\alpha0_s \sim Normal(\mu_{\alpha0}, \sigma_{\alpha0}^2)\)). Using alpha0 as an example we code this as:

alpha0[s] ~ dnorm(mu_a0, tau_a0)

mu_a0 ~ dnorm(0, 0.01)
tau_a0 ~ dgamma(0.1, 0.1)
sig_a0 <- 1/sqrt(tau_a0)

This allows information between species to be shared, but we still have species-specific estimates of each parameter.

Miscellaneous: Negative Binomial as Poisson-gamma mixture

A miscellaneous topic that I would like to address is the specification of the negative binomial as a Poisson-gamma mixture. We first used a negative binomial for both abundance/number of groups and group size to account for overdispersion. We use a Poisson-gamma mixture, which is an alternate specification of the negative binomial. The JAGS built-in dnegbin uses the classic specification, but the Poisson-gamma mixture is more convenient for our use. The code for this is:

N[i] ~ dpois(lambda[i]*rho[i])
rho[i] ~ dgamma(r, r)
r ~ dgamma(0.1, 0.1)

rho[i] is our dispersion parameter, which is the realization of a gamma distribution. For more information see Greene (2008) or this forum on sourceforge.net.